Reachability of Koopman Linearized Systems Using Random Fourier Feature Observables and Polynomial Zonotope Refinement

Abstract

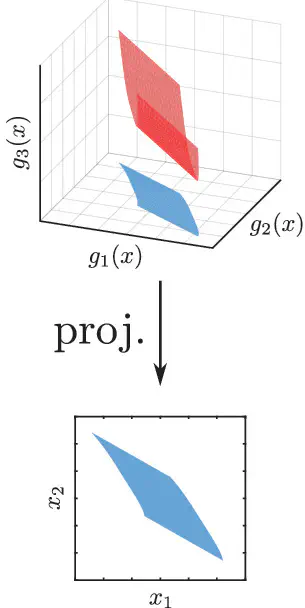
Koopman operator linearization approximates nonlinear systems of differential equations with higher-dimensional linear systems. For formal verification using reachability analysis, this is an attractive conversion, as highly scalable methods exist to compute reachable sets for linear systems. However, two main challenges are present with this approach, both of which are addressed in this work. First, the approximation must be sufficiently accurate for the result to be meaningful, which is controlled by the choice of observable functions during Koopman operator linearization. By using random Fourier features as observable functions, the process becomes more systematic than earlier work, while providing a higher-accuracy approximation. Second, although the higher-dimensional system is linear, simple convex initial sets in the original space can become complex non-convex initial sets in the linear system. We overcome this using a combination of Taylor model arithmetic and polynomial zonotope refinement. Compared with prior work, the result is more efficient, more systematic and more accurate.