Abstract
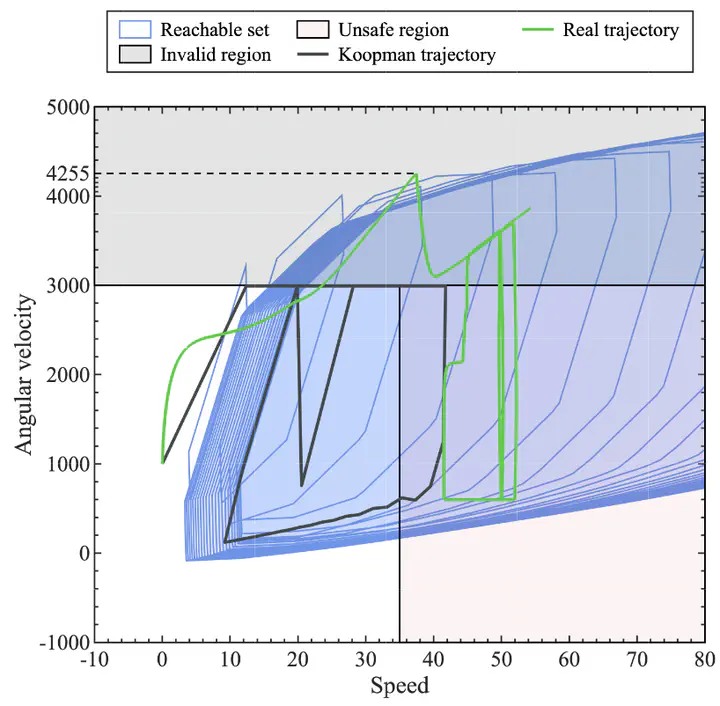
Black-box falsification problems are most often solved by numerical optimization algorithms. In this work, we propose an alternative approach, where simulations are used to construct a surrogate model for the system dynamics using data-driven Koopman operator linearization. Since the dynamics of the Koopman model are linear, the reachable set of states can be computed and combined with an encoding of the signal temporal logic specification in a mixed-integer linear program (MILP). To determine the next sample, an MILP solver computes the least robust trajectory inside the reachable set of the surrogate model. The trajectory’s initial state and input signal are then executed on the original black-box system, where the specification is either falsified or additional simulation data is generated that we use to retrain the surrogate Koopman model and repeat the process.